
Méthodes de simplification algébrique
Les règles fondamentales permettant de simplifier une équation logique de façon algébrique sont représentées ci-contre. Ces règles sont issues de l'algèbre de Boole.
Une algèbre
est booléenne si elle dispose de deux opérations (ici + et .)
qui sont :
- des lois internes,
- commutatives, et associatives,
- disposant chacune d'un élément neutre,
- distributives l'une par rapport à l'autre.
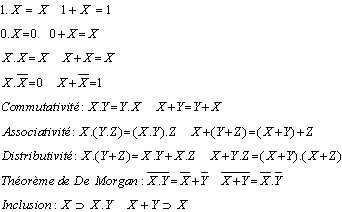
Chaque élement de B={0,1} possède en outre un complément unique : 1 est le complément de 0 et vice-versa.
Ces lois appliquées
méthodiquement à une équation de départ, permettent
sa simplification :
- l'absorption
permet d'ajouter des termes.
Exemple X.Y.Z étant contenu dans X.Z, on peut écrire : X.Z
= X.Z + X.Y.Z
- la distributivité permet
de regrouper des termes (voir ci-dessus), etc.
Les méthodes
de simplification algébriques procèdent en deux temps:
- recherche des intersections premières,
- recherche de la réunion permettant d'obtenir le plus petit nombre
possible d'intersections premières. On l'appelle réunion
minimale.
Ces méthodes algébriques (Quine-McCluskey et Tison) sont beaucoup plus lourdes que les méthodes graphiques (tableaux de Karnaugh en particulier), et n'offrent donc pas beaucoup d'intérêt pour l'ingénieur. Elles peuvent toutefois être utilisées dans les calculateurs, une fois les choix technologiques connus.