Page 3 - Filtrage numérique

Version 1.0.0 du 1/10/2006 Le Filtrage numérique
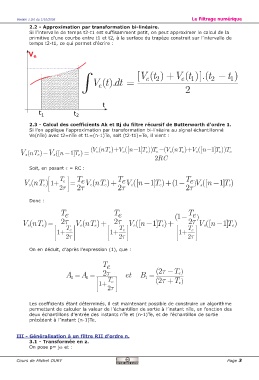
2.2 - Approximation par transformation bi-linéaire.
Si l’intervalle de temps t2-t1 est suffisamment petit, on peut approximer le calcul de la
primitive d’une courbe entre t1 et t2, à la surface du trapèze construit sur l’intervalle de
temps t2-t1, ce qui permet d’écrire :
V e

∫ Vt [ ()Vt + Vt 1 ] ) .(t − t 1 )
(
().dt =
2
e
2
e
e
2
t
t 1 t 2

2.3 - Calcul des coefficients Ak et Bj du filtre récursif de Butterworth d’ordre 1.
Si l’on applique l’approximation par transformation bi-linéaire au signal échantillonné
Ve(nTe) avec t2=nTe et t1=(n-1)Te, soit (t2-t1)=Te, il vient :

V s (nT e ) V− s ([n − 1] )T = ( (VnT e ) V+ e ([n− 1] ))T T − ( (V nT e ) V+ s ([n− 1] ))T T e
e
e
e
e
s
e
2RC
Soit, en posant τ = RC :
⎡ T e ⎤ T T T
(
)
s V
s VnT e ⎢ 1+ ⎥ = e e V (nT e )+ e e V ([n − 1] ) (1+ − e ) ([n − 1] )
e T
e T
⎢ ⎣ 2τ ⎥ ⎦ 2τ 2τ 2τ
Donc :
T e T e (1− T e )
e T
e T
(
s VnT e )= 2τ e V (nT e )+ 2τ e V ([n − 1] )+ 2τ s V ([n − 1] )
⎡ T e ⎤ ⎡ T e ⎤ ⎡ T e ⎤
⎢ 1+ ⎥ ⎢ 1+ ⎥ ⎢ 1+ ⎥
⎢ ⎣ 2τ ⎥ ⎦ ⎢ ⎣ 2τ ⎥ ⎦ ⎢ ⎣ 2τ ⎥ ⎦
On en déduit, d’après l’expression (1), que :

T e

A = A = 2τ et B = (2τ − e T )
0 1 ⎡ T e ⎤ 1 (2τ +
⎢ 1+ ⎥ e T )
⎢ ⎣ 2τ ⎥ ⎦

Les coefficients étant déterminés, il est maintenant possible de construire un algorithme
permettant de calculer la valeur de l’échantillon de sortie à l’instant nTe, en fonction des
deux échantillons d’entrée des instants nTe et (n-1)Te, et de l’échantillon de sortie
précédant à l’instant (n-1)Te.

III - Généralisation à un filtre RII d’ordre n.
3.1 - Transformée en z.
On pose p= jω et :

Cours de Michel OURY Page 3