Page 3 - Acquisition et traitement du signal

Version 1.1.0 du 23/9/2006 Acquisition et traitement du signal
La propriété essentielle du signal v(t) est le plus souvent contenue dans les harmoniques 1,
2, ou 3 s’ils existent.

On peut également écrire :
∞
c ∑
() =
vt v + C n .cos (n tω + ϕ n )
n= 1

avec C = A + B 2
2
n n n

⎛ B ⎞
et ϕ = Arctg ⎜ n ⎟
n
⎝ A n ⎠
Cet ϕ
n n représentent respectivement le module et la phase de l’harmonique de rang n.

Remarque : On montrera que le développement en série de Fourier d’une fonction paire
(impaire) ne contient pas de termes en sinus (cosinus).
Il est également possible de la même façon de synthétiser un signal périodique en faisant la
somme de ses n premiers harmoniques non nuls (n variable de 3 à 7 est suffisant).

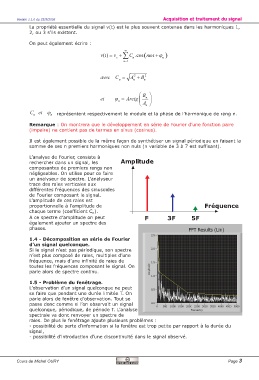
L’analyse de Fourier, consiste à
rechercher dans un signal, les Amplitude
composantes de premiers rangs non
négligeables. On utilise pour ce faire
un analyseur de spectre. L’analyseur
trace des raies verticales aux
différentes fréquences des sinusoïdes
de Fourier composant le signal.
L’amplitude de ces raies est
proportionnelle à l’amplitude de Fréquence
chaque terme (coefficient C ).
n
A ce spectre d’amplitude on peut F 3F 5F
également ajouter un spectre des
phases.

1.4 - Décomposition en série de Fourier
d’un signal quelconque.
Si le signal n’est pas périodique, son spectre
n’est plus composé de raies, multiples d’une
fréquence, mais d’une infinité de raies de
toutes les fréquences composant le signal. On
parle alors de spectre continu.

1.5 - Problème du fenêtrage.
L’observation d’un signal quelconque ne peut
se faire que pendant une durée limitée T. On
parle alors de fenêtre d’observation. Tout se
passe donc comme si l’on observait un signal
quelconque, périodique, de période T. L’analyse
spectrale va donc renvoyer un spectre de
raies. De plus le fenêtrage ajoute plusieurs problèmes :
- possibilité de perte d’information si la fenêtre est trop petite par rapport à la durée du
signal,
- possibilité d’introduction d’une discontinuité dans le signal observé.

Cours de Michel OURY Page 3