Page 6 - Acquisition et traitement du signal

Version 1.1.0 du 23/9/2006 Acquisition et traitement du signal

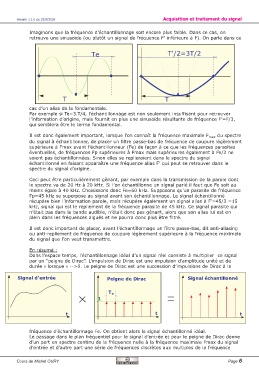
Imaginons que la fréquence d’échantillonnage soit encore plus faible. Dans ce cas, on
retrouve une sinusoïde (ou plutôt un signal de fréquence F’ inférieure à F). On parle dans ce

Te T'/2=3T/2

T T

cas d’un alias de la fondamentale.
Par exemple si Te=3.T/4, l’échantillonnage est non seulement insuffisant pour retrouver
l’information d’origine, mais fournit en plus une sinusoïde résultante de fréquence F’=F/3,
qui semblera être le terme fondamental.

Il est donc également important, lorsque l’on connaît la fréquence maximale F max du spectre
du signal à échantillonner, de placer un filtre passe-bas de fréquence de coupure légèrement
supérieure à Fmax avant l’échantillonneur (Fe) de façon à ce que les fréquences parasites
éventuelles, de fréquences Fp supérieures à Fmax mais supérieures également à Fe/2 ne
soient pas échantillonnées. Sinon elles se replieraient dans le spectre du signal
échantillonné en faisant apparaître une fréquence alias F’ qui peut se retrouver dans le
spectre du signal d’origine.

Ceci peut être particulièrement gênant, par exemple dans la transmission de la parole dont
le spectre va de 20 Hz à 20 kHz. Si l’on échantillonne un signal parlé il faut que Fe soit au
moins égale à 40 kHz. Choisissons donc Fe=60 kHz. Supposons qu’un parasite de fréquence
Fp=45 kHz se superpose au signal avant son échantillonnage. Le signal échantillonné
récupère bien l’information parole, mais récupère également un signal alias à F’=45/3 =15
kHz, signal qui est le repliement de la fréquence parasite de 45 kHz. Ce signal parasite qui
n’était pas dans la bande audible, n’était donc pas gênant, alors que son alias lui est en
plein dans les fréquences aiguës et ne pourra donc plus être filtré.

Il est donc important de placer, avant l’échantillonnage un filtre passe-bas, dit anti-aliasing
ou anti-repliement de fréquence de coupure légèrement supérieure à la fréquence maximale
du signal que l’on veut transmettre.

En résumé :
Dans l’espace temps, l’échantillonnage idéal d’un signal réel consiste à multiplier ce signal
par un “peigne de Dirac”. L’impulsion de Dirac est une impulsion d’amplitude unité et de
durée τ lorsque τ -->0. Le peigne de Dirac est une succession d’impulsions de Dirac à la

Signal d'entrée Peigne de Dirac Signal échantillonné

T e
1

t t t

fréquence d’échantillonnage Fe. On obtient alors le signal échantillonné idéal.
Le passage dans le plan fréquentiel pour le signal d’entrée et pour le peigne de Dirac donne
d’un part un spectre continu de la fréquence nulle à la fréquence maximale Fmax du signal
d’entrée et d’autre part une série de fréquences discrètes aux multiples de la fréquence

Cours de Michel OURY Page 6