Page 5 - Acquisition et traitement du signal
P. 5
Version 1.1.0 du 23/9/2006 Acquisition et traitement du signal
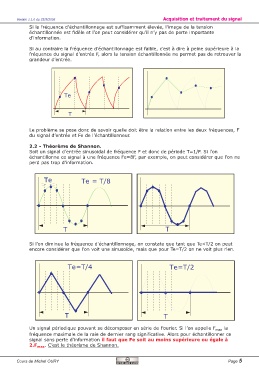
Si la fréquence d’échantillonnage est suffisamment élevée, l’image de la tension
échantillonnée est fidèle et l’on peut considérer qu’il n’y pas de perte importante
d’information.
Si au contraire la fréquence d’échantillonnage est faible, c’est à dire à peine supérieure à la
fréquence du signal d’entrée F, alors la tension échantillonnée ne permet pas de retrouver la
grandeur d’entrée.
Te
T
Le problème se pose donc de savoir quelle doit être la relation entre les deux fréquences, F
du signal d’entrée et Fe de l’échantillonneur.
2.2 - Théorème de Shannon.
Soit un signal d’entrée sinusoïdal de fréquence F et donc de période T=1/F. Si l’on
échantillonne ce signal à une fréquence Fe=8F, par exemple, on peut considérer que l’on ne
perd pas trop d’information.
Te Te = T/8
T T
Si l’on diminue la fréquence d'échantillonnage, on constate que tant que Te<T/2 on peut
encore considérer que l’on voit une sinusoïde, mais que pour Te=T/2 on ne voit plus rien.
Te=T/4 Te=T/2
T T
Un signal périodique pouvant se décomposer en série de Fourier. Si l’on appelle F max la
fréquence maximale de la raie de dernier rang significative. Alors pour échantillonner ce
signal sans perte d’information il faut que Fe soit au moins supérieure ou égale à
2.F max . C’est le théorème de Shannon.
Cours de Michel OURY Page 5