Page 7 - Acquisition et traitement du signal

Version 1.1.0 du 23/9/2006 Acquisition et traitement du signal
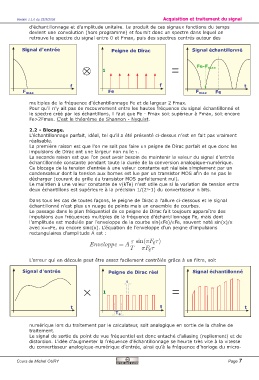
d’échantillonnage et d’amplitude unitaire. Le produit de ces signaux fonctions du temps
devient une convolution (hors programme) et fournit donc un spectre dans lequel on
retrouve le spectre du signal entre 0 et Fmax, puis des spectres centrés autour des

Signal d'entrée Peigne de Dirac Signal échantillonné

Fe-F max
1

f f t
F max Fe F max Fe

multiples de la fréquence d'échantillonnage Fe et de largeur 2 Fmax.
Pour qu’il n’y ait pas de recouvrement entre les hautes fréquence du signal échantillonné et
le spectre créé par les échantillons, il faut que Fe - Fmax soit supérieur à Fmax, soit encore
Fe>2Fmax. C’est le théorème de Shannon - Nyquist.

2.2 - Blocage.
L’échantillonnage parfait, idéal, tel qu’il a été présenté ci-dessus n’est en fait pas vraiment
réalisable.
La première raison est que l’on ne sait pas faire un peigne de Dirac parfait et que donc les
impulsions de Dirac ont une largeur non nulle τ.
La seconde raison est que l’on peut avoir besoin de maintenir la valeur du signal d’entrée
échantillonnée constante pendant toute la durée de la conversion analogique-numérique.
Ce blocage de la tension d’entrée à une valeur constante est réalisée simplement par un
condensateur dont la tension aux bornes est lue par un transistor MOS afin de ne pas le
décharger (courant de grille du transistor MOS parfaitement nul).
Le maintien à une valeur constante de v(kTe) n’est utile que si la variation de tension entre
n
deux échantillons est supérieure à la précision 1/(2 -1) du convertisseur n bits.
Dans tous les cas de toutes façons, le peigne de Dirac a l’allure ci-dessous et le signal
échantillonné n’est plus un nuage de points mais un ensemble de courbes.
Le passage dans le plan fréquentiel de ce peigne de Dirac fait toujours apparaître des
impulsions aux fréquences multiples de la fréquence d'échantillonnage Fe, mais dont
l’amplitude est modulée par l’enveloppe de la courbe sin(πFe)/πFe, souvent noté sin(x)/x
avec x=πFe, ou encore sinc(x). L’équation de l’enveloppe d’un peigne d’impulsions
rectangulaires d’amplitude A est :
πτ
Enveloppe = A τ sin( F e )
T πτ
F
e
L’erreur qui en découle peut être assez facilement contrôlée grâce à un filtre, soit

Signal d'entrée Peigne de Dirac réel Signal échantillonné
τ τ

1

t t t
T e

numérique lors du traitement par le calculateur, soit analogique en sortie de la chaîne de
traitement.
Le signal de sortie du point de vue fréquentiel est donc entaché d’aliasing (repliement) et de
distorsion. L’idée d’augmenter la fréquence d’échantillonnage se heurte très vite à la vitesse
du convertisseur analogique-numérique d’entrée, ainsi qu’à la fréquence d’horloge du micro-

Cours de Michel OURY Page 7